How To Use The Rule Of 78 Interest

When lenders use the Rule of 78's, they distribute the total finance charge over all payments, but charge more interest early in the loan period and less later, compared to other methods. The Rule of 78's is also called the "sum of digits" because it gets its name from summing the digits 1 through 12 - the number of months in a one year loan. Yes, this is 78.

Here is how the Rule of 78's is applied to a Amortized loan. Interest is calculated as described in the topic Amortized Loan - Normal. (The formulas are repeated below but you will have to refer to the aforementioned topic for details.)

Payment Amount

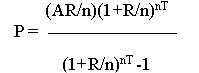
P = Payment
A = Amount borrowed
R = Annual Interest Rate
n = number of compound payments per year.
T = time in years.
nT = Term, the total number of payments in the loan schedule. This is the number of periods per year multiplied by the number of years. This is the exponent. In the formula, 1 + the Interest Rate(R/n) is multiplied by itself as many times as the value of the Term(nT).

Total Plan Payments

TP = P x T

TP = Total Plan Payments
P = Payment Amount
T = number of Payments (Term)

Total Interest

TI = TP - A

TI = Total Interest
TP = Total Plan Payments
A = Amount Borrowed

When you know the Total Interest through the calculations above, you can calculate interest rebate using Rule of 78's.

Interest Payments

First, you need the Sum of the number of payments.

For instance, if the Term is 12 monthly payments, the summation of 12 payments is

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78

The amount of interest to be paid per payment is calculated as follows.

12/78 x Total Interest = First Payment
11/78 x Total Interest = Second Payment
- and so on until...1/78 x Total Interest = Final Payment

This rule applies to long term loans the same way.

For example, a 24-month loan - where the sum of the digits 1 through 24 is 300 - would have a first month's interest payment that is 24/300 of the total interest. The second month would be 23/300 and so on.

A three year loan, 36 months - where the sum of the digits 1 through 36 is 666 - would have a first month's interest payment that is 36/666 of the total interest, second month would be 35/666 and so on.

The above fractions are applied to the Total Interest amount. The remainder of the Payment amount would be applied to outstanding principal. As the months go by, the interest portion decreases and the principal is paid off faster. However, the interest portion is a fixed amount determined by the Rule of 78's. It is not recalculated each time from outstanding principal.

The amount applied to Principal is

Payment Amount - Interest for Payment = Applied to Principal.

Early Payout Amount

If the loan is paid off before the full Term has expired, there is usually an interest rebate. The borrower did not have the money as long as originally planned and did not accumulate as much interest on the loan. However, the lender depends on the interest as payment for lending money. This is the financial charge of the loan. If a loan is paid off early, the portion of interest that is left is less with Rule of 78's and this benefits the lender.

For instance, if a 12-month loan is paid in 10 months,

2/78 of the Total Interest - the 11th payment and
1/78 of the Total Interest - the 12th and final payment

is all the remaining financial charge left unpaid. So 75/78 of the Total Interest has already been paid. Only 3/78 of the Total Interest is saved by paying the loan early.

To calculate the Early Payout Amount, first determine the number of payments remaining. Then calculate the Interest amount saved as shown above.

It is very straightforward:

1. Each payment is numbered from 1 to the total number in the Term. (12 or 24 or 36 or whatever)

2. The bottom part of the fraction is figured by "summing the digits." (78 or 300 or 666 or whatever)

3. Interest left to pay is calculated as described above.

If a 36-month loan is paid in 30 months, for instance, the amount of interest left to be refunded or deducted from the total outstanding debt is the following.

1/666 of the Total Interest + 2/666 of the Total Interest + 3/666 of the Total Interest + 4/666 of the Total Interest + 5/666 of the Total Interest + 6/666 of the Total Interest = 21/666 of the Total Interest that must be rebated to the borrower.

This is the Interest Amount Saved and is used to calculate Early Payout Amount.

Early Payout Amount = OP + TI - IAS - PP - IP

OP = Original Principal
TI = Total Interest
IAS = Interest Amount Saved
PP = Principal Paid
IP = Interest Paid

Another formula which gives the Interest Amount Saved is the following.

(No. of months remaining + 1) x (No. of months remaining)
divided by (No. of months in Term + 1) x (No. of months in Term)

This gives the same result as above.

Early Payoff Penalty

When a loan is paid off a great deal sooner than expected, the borrower can actually experience a penalty. This is because Rule of 78's calculates higher interest percentages in earlier months than other types of calculating. This interest is still due according to the agreement made, even though the actual calculation of interest would not be as high.

For instance, borrowing $10,000 for two years at 12% would amount to $1297.65 in Total Interest (using a 365 day year.)

If this loan is paid after only four months, the actual interest on the amount and the length of time would be $377.61.

Using Rule of 78's, the interest charge for the first four months amounts to $389.30. (Using the formulas given above.)

This is an additional 3% interest.

As a rule:

1. The higher the interest rate, the greater the penalty amount. 2. The earlier the prepayment in relation to the term, the greater the penalty amount.

So, if you are a lender, you benefit from Rule of 78's. If you are a borrower, you should try to avoid it.

WARNING: Some states have usury and other laws that may limit the use of the Rule of 78's.

Rate Basis

For "Rule of 78" accounts, the Rate Basis is only a factor if the first payment is deferred. A deferred payment is a payment where the First Payment Date is more than one Period away from the Calculate Interest From Date. Interest is calculated on this difference and the current Rate Basis is a factor in this calculation.