How To Use Amortized Loan - Normal Interest

The most common method of repaying an interest-bearing loan is by amortization. In this method, a series of periodic payments is made. The indebtedness at any time is called the outstanding balance or outstanding principal. It is just the discounted value of all unmade payments.

Each sequential payment pays the interest on the unpaid balance and also repays a part of the outstanding principal. Over the term of the loan, as the outstanding principal decreases, the interest portion of each payment decreases and the principal portion increases. This shifting distribution is shown in an amortization schedule. Amortized loan is calculated according to this schedule. Payments are set up using the formula given below.

RULE OF 78's

The difference between the above method and Rule of 78's is that, in the Rule of 78's, the interest portion of each payment is not determined by the unpaid balance, but rather by a calculation which is called Rule of 78's. This may result in a different distribution shift than described above. As well, if a loan is paid off early, with Rule of 78's computing, a borrower

does not receive as much of an interest refund as in other forms of borrowing.

Please see How to Use the Rule of 78 Interest for details and formulas used in this type of calculation.

Amortized Loan Information

In the Interest Detail form, the Operator enters:

Annual Interest Rate - as a percent, e.g. 15. This is the Annual rate of interest. When Period is more frequent than Annual, Interest rates are calculated for the Period using the formula -- R/n

Period - pick a Period from the list. This is a frequency of interest conversion (compounding) and a frequency of payment. Collect! uses this information to determine how often to compound Interest. It also states how often a debtor is scheduled to make a payment.

Rate Basis - 360, 364 or 365 days, or Ordinary - 12 months. This is the length of the year.

Calculate Interest From Date - the date you want calculation to begin.

Term - this is the Total Number of Payments. It is NOT in the formula below. If the debtor is paying monthly for four years, that means 12 payments for 4 years so Term = 48.

First Payment Date - the date you want the first payment to be due.

These are the basic values that Collect! needs to set up the pre-amortization schedule and display results of calculations. There are additional options you can choose. Press F1 in the Interest Detail form for information on the field you are wondering about.

Payment Amount

Collect! uses the following formula to calculate Payment amount. The Operator enters the information listed above and Collect! performs the necessary calculations.

Payment Amount

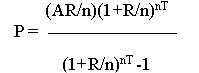
P = Payment

A = Amount borrowed

R = Annual Interest Rate

n = number of compound payments per year. This is how often the interest is compounded, (the Period.) (e.g. Quarterly period: n = 4, Bimonthly period: n = 6)

R/n = the Interest Rate of a Compounding Period. This divides the Annual rate by the number of times a year the interest is compounded (the number of periods.)

T = time in years. This is the number of years allowed to pay off the loan. This calculation takes into consideration the Rate Basis set in the Interest Detail.

nT = Term, the total number of payments in the loan schedule. This is the number of periods per year multiplied by the number of years. This is the exponent. In the formula, 1 + the Interest Rate(R/n) is multiplied by itself as many times as the value of the Term(nT).

Example:

$2000 borrowed at 5% for 2 years with Monthly payments.

Plugged into the formula:

((2000 x .05) / 12) x (1 + .05 / 12) (multiplied by itself 24 times) Divided by (1 + .05 / 12) (multiplied by itself 24 times) minus 1

Approximately, this results in 8.3333 x 1.10494 divided by .10494 which gives a monthly payment of $87.74.

Total Plan Payments

Total Plan Payments amount is calculated as follows:

TP = P x T

TP = Total Plan Payments
P = Payment Amount
T = number of Payments (Term)

In our example, this is 87.74 x 24 = $2105.76

If the Set Terms Manually switch is ON, the Payment Amount is supplied and Payment Amount formula is not used.

Total Interest

To calculate the Total Interest, the following is used:

TI = TP - A

TI = Total Interest
TP = Total Plan Payments
A = Amount Borrowed

In our example, this is 2105.76 - 2000 = $105.76

Time In Years

Calculations take into consideration the Rate Basis set in the Interest Detail. This Rate Basis is used in every single interest

calculation. It can be set to Ordinary, 360, 364 or 365 days.